Table des matières
Introduction : La géométrie à votre portée
Comprendre comment calculer l’aire d’un triangle est une compétence essentielle que l’on retrouve dans de nombreux domaines : éducation, architecture, design, bricolage ou encore jardinage. Que vous soyez élève, parent, enseignant, amateur de mathématiques ou professionnel, cette notion vous servira pour résoudre des problèmes concrets et variés.
Mais attention, il n’existe pas qu’une seule manière de calculer cette fameuse aire. Selon les informations disponibles sur le triangle à étudier (longueurs, angles, types de triangle), plusieurs méthodes s’offrent à vous. Certaines sont simples, d’autres plus techniques, mais toutes mènent au même résultat.
Dans cet article ultra-détaillé, nous vous présentons toutes les techniques pour calculer l’aire d’un triangle, accompagnées d’exemples concrets, de tableaux comparatifs, d’astuces et d’exercices pratiques.
Définition de l’aire d’un triangle
L’aire d’un triangle est la mesure de la surface comprise à l’intérieur de ses trois côtés. Elle est exprimée en unités carrées (cm², m², km²…) et permet d’évaluer la superficie du triangle.
Formule de base :
Aire = \frac{base \times hauteur}{2}Cette formule simple est valable pour tous les triangles, à condition de connaître une base et la hauteur correspondante.
Méthode 1 : Avec la base et la hauteur
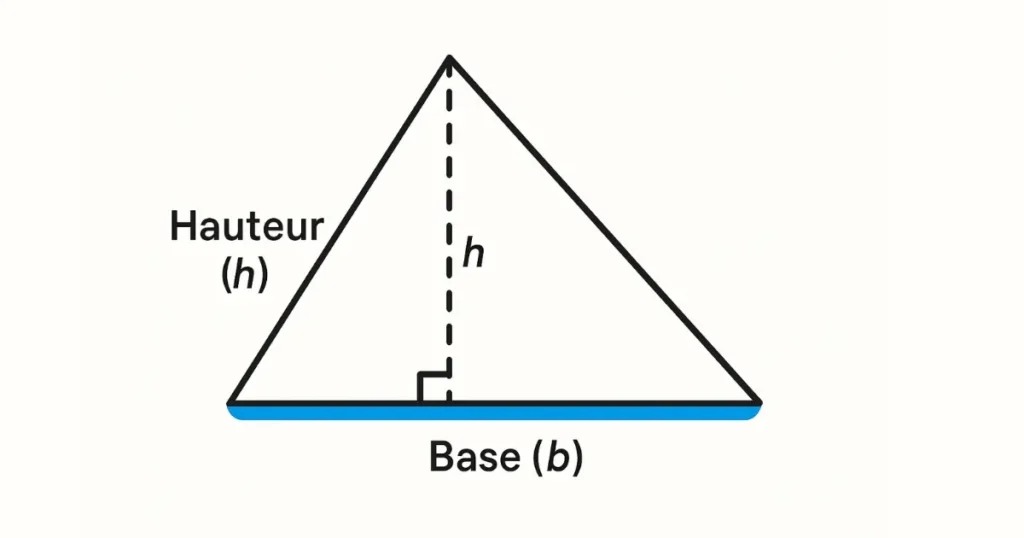
Il s’agit de la méthode la plus intuitive et la plus utilisée, notamment pour les triangles rectangles ou les triangles facilement mesurables.
✅ Formule :
A = \frac{b \times h}{2}- b : base du triangle (l’un des côtés)
- h : hauteur perpendiculaire à cette base
🔢 Exemple :
Un triangle a pour base 8 cm et pour hauteur 5 cm.
A = \frac{8 \times 5}{2} = \frac{40}{2} = 20 , \text{cm}^2Astuce : Il est essentiel de veiller à ce que la hauteur soit perpendiculaire à la base !
Méthode 2 : Formule de Héron (quand la hauteur est inconnue)
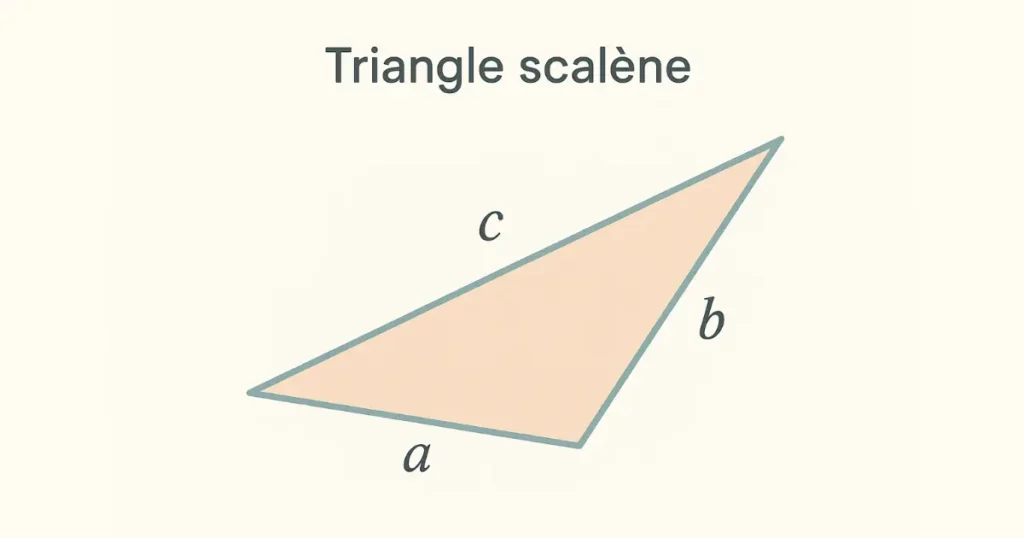
La formule de Héron est particulièrement utile lorsque vous connaissez les longueurs des trois côtés du triangle, mais que la hauteur est impossible à mesurer.
✅ Étapes :
- Calculez le demi-périmètre :
Appliquez la formule :
A = \sqrt{s(s - a)(s - b)(s - c)}🔢 Exemple :
Triangle avec a = 5 cm, b = 6 cm, c = 7 cm
s = 9 A = \sqrt{9(9-5)(9-6)(9-7)} = \sqrt{216} \approx 14,7 , \text{cm}^2Remarque : Cette méthode est efficace, mais demande un peu plus de calculs.
Méthode 3 : Avec un angle connu
Si vous connaissez deux côtés et l’angle compris entre eux, utilisez cette formule trigonométrique.
✅ Formule :
A = \frac{1}{2}ab \sin(C)- a et b : côtés du triangle
- C : angle compris entre a et b
🔢 Exemple :
Côtés a = 7 cm, b = 10 cm, angle C = 30°
A = \frac{1}{2} \times 7 \times 10 \times \sin(30\degree) = 17,5 , \text{cm}^2Astuce : Vérifiez bien que votre calculatrice est en mode degrés ou radians selon l’angle.
Tableau comparatif des méthodes
| Méthode | Données requises | Formule | Utilisation recommandée |
|---|---|---|---|
| Base et hauteur | b, h | A = \frac{b \times h}{2} | Triangle rectangle, données simples |
| Formule de Héron | Trois côtés (a, b, c) | A = \sqrt{s(s-a)(s-b)(s-c)} | Pas de hauteur connue |
| Trigonométrie | 2 côtés + angle (C) | A = \frac{1}{2}ab\sin(C) | Triangle quelconque avec angle connu |
Quiz : Testez vos compétences
Question 1 : Un triangle a une base de 12 cm et une hauteur de 4 cm. Quelle est son aire ?
A) 48 cm²
B) 24 cm²
C) 12 cm²
Question 2 : Si les côtés d’un triangle sont 6 cm, 8 cm et 10 cm, quelle formule devez-vous utiliser ?
A) Trigonométrie
B) Héron
C) Base × Hauteur
Question 3 : Un triangle a des côtés de 9 cm et 12 cm avec un angle de 60°. Quelle méthode appliquer ?
A) Trigonométrie
B) Héron
C) Coordonnées
Réponses du quiz
- B : \frac{12 \times 4}{2} = 24 , \text{cm}^2
- B : Formule de Héron (trois côtés connus)
- A : Trigonométrie (2 côtés et un angle donné)
Cas particuliers : quand le triangle est spécial
Triangle rectangle
Le triangle rectangle est l’un des plus simples pour calculer l’aire :
A = \frac{côté_{adjacent} \times côté_{opposé}}{2}Exemple : côtés de 3 cm et 4 cm
A = 6 , \text{cm}^2Triangle équilatéral
Tous les côtés égaux → formule spécifique :
A = \frac{\sqrt{3}}{4} \times c^2Exemple : c = 6 cm → A \approx 15,6 , \text{cm}^2
Triangle en coordonnées (x, y)
Utilisez la formule vectorielle :
A = \frac{1}{2} \left| x_1(y_2 - y_3) + x_2(y_3 - y_1) + x_3(y_1 - y_2) \right|FAQ : Calcul de l’air des triangles
Peut-on appliquer n’importe quelle formule à tous les triangles ?
Non. Cela dépend des informations connues sur le triangle : côtés, hauteur, angle, type de triangle, etc.
Quelle est l’unité d’aire dans un triangle ?
Comme pour toute surface : cm², m², mm², etc. Tout dépend de l’unité de mesure utilisée pour les longueurs.
Comment calculer l’aire d’un triangle isocèle ?
S’il est possible d’en déduire la hauteur, utilisez la formule classique. Sinon, utilisez la trigonométrie ou Héron.
✅ Points clés: ce qu’il faut retenir
- Utilisez la formule classique si vous connaissez la base et la hauteur.
- Optez pour Héron si vous connaissez les trois côtés.
- Appliquez la trigonométrie si vous avez deux côtés et un angle.
- Adaptez votre méthode au type de triangle.
- N’oubliez pas les unités en surface carrée !
Conclusion : Comment calculer l’aire d’un triangle ?
Calculer l’aire d’un triangle n’est plus un mystère une fois que l’on connaît les bonnes formules et qu’on sait les adapter aux données disponibles. Que vous disposiez de la base et de la hauteur, des trois côtés ou encore de deux côtés avec un angle, il existe toujours une méthode efficace et précise pour obtenir le bon résultat. Grâce aux outils mathématiques comme la formule classique, celle de Héron ou la trigonométrie, vous êtes désormais capable de répondre à la question essentielle : comment calculer l’aire d’un triangle ? Avec un peu de pratique, ce calcul deviendra aussi naturel que rapide, que ce soit pour un usage scolaire, professionnel ou personnel.