Table des matières
Quand deux droites parallèles sont coupées par une transversale, une drôle de géométrie s’installe… et il faut savoir repérer les angles alternes-internes et les angles correspondants pour ne pas s’emmêler les crayons ! Ces notions sont fondamentales en géométrie, car elles permettent de démontrer des égalités d’angles et de comprendre la logique des figures planes. C’est une compétence de base indispensable pour réussir en mathématiques, notamment dans les programmes du collège et du lycée.
Voici le guide express, visuel, pédagogique et ludique, pour tout comprendre avec des explications claires un quiz , des schémas et un exercice pour devenir un pro de ces configurations. Grâce à ce tutoriel, tu n’auras plus aucun doute en géométrie ! Que tu sois en cours de maths, en révision pour un contrôle ou simplement curieux, ce guide est fait pour toi.
Comprendre les angles formés par une transversale
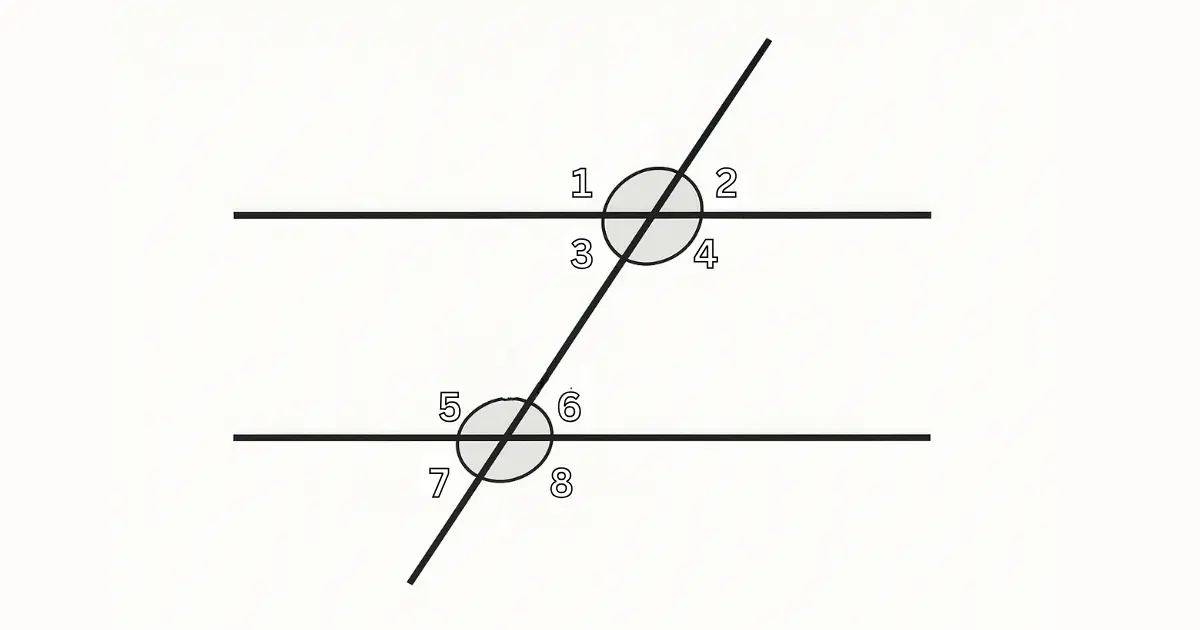
Lorsqu’une transversale traverse deux droites parallèles, elle coupe ces deux droites en formant huit angles distincts. Ces angles apparaissent en paires selon leur position relative à la transversale et aux droites parallèles. Certains se trouvent à l’intérieur des droites, d’autres à l’extérieur. En observant bien leurs positions, on peut identifier des paires d’angles égaux selon des règles précises.
Ces relations sont à la base de nombreux raisonnements en géométrie. Elles sont utilisées pour démontrer que deux lignes sont parallèles, pour calculer des angles inconnus ou encore pour justifier des constructions géométriques.
Définition des angles alternes-internes
- Ils sont situés à l’intérieur des deux droites parallèles.
- Ils se trouvent de part et d’autre de la transversale, c’est-à-dire un à gauche et un à droite.
- Ils n’ont pas de sommet commun et forment un « Z » imaginaire.
👉 Ils sont égaux si les droites sont parallèles. Cette égalité d’angles est essentielle pour justifier qu’un quadrilatère est un parallélogramme, par exemple.
Exemple :
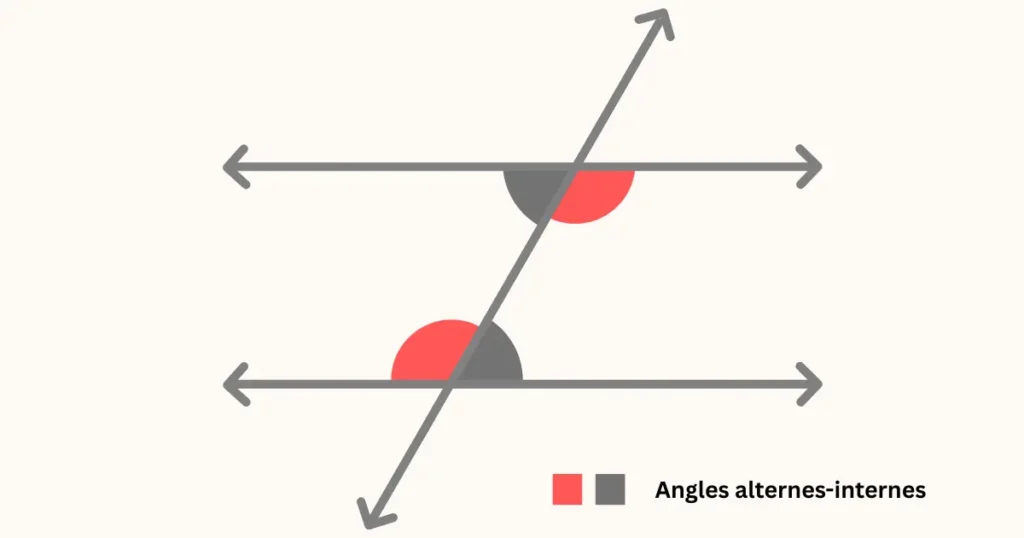
Il suffit de tracer un « Z » ou un « S » inversé pour les visualiser facilement. On retrouve ces configurations dans les triangles, les quadrilatères et même dans les constructions de figures complexes.
Exemples d’utilisation :
- Démontrer que deux droites sont parallèles.
- Identifier des propriétés d’un parallélogramme.
- Résoudre un problème de calcul d’angles.
Définition des angles correspondants
- Ils sont du même côté de la transversale.
- L’un est à l’intérieur, l’autre à l’extérieur des droites.
- Ils sont placés dans une position identique (même coin) par rapport aux deux droites.
👉 Ils sont égaux si les droites sont parallèles. Ils permettent souvent de justifier des angles dans des figures symétriques.
Exemple :
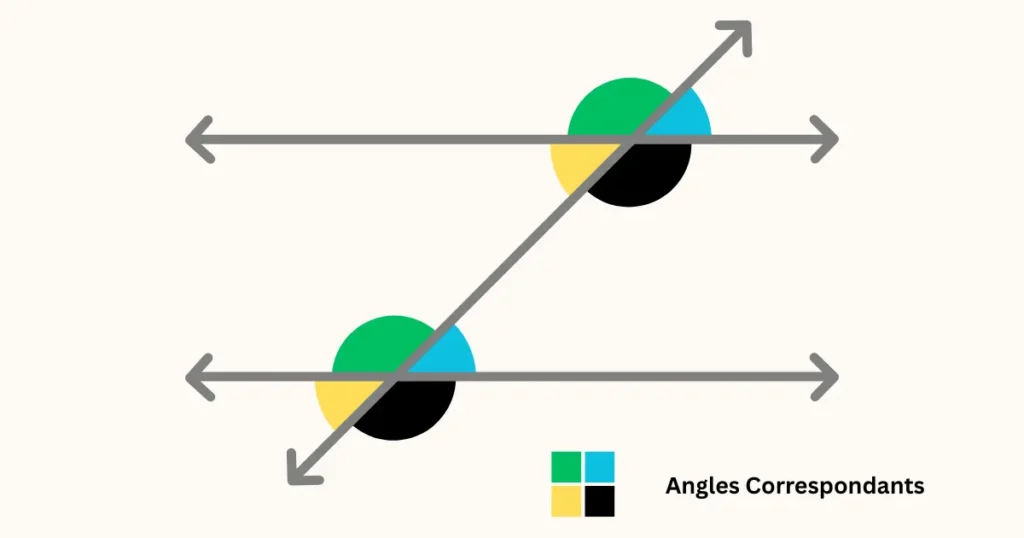
On peut aussi se représenter un « F » ou un « E » renversé pour les repérer rapidement.
Cas concrets :
- Identifier des angles égaux dans une figure symétrique.
- Comparer des positions équivalentes dans deux zones d’une figure.
- Construire des figures géométriques avec précision.
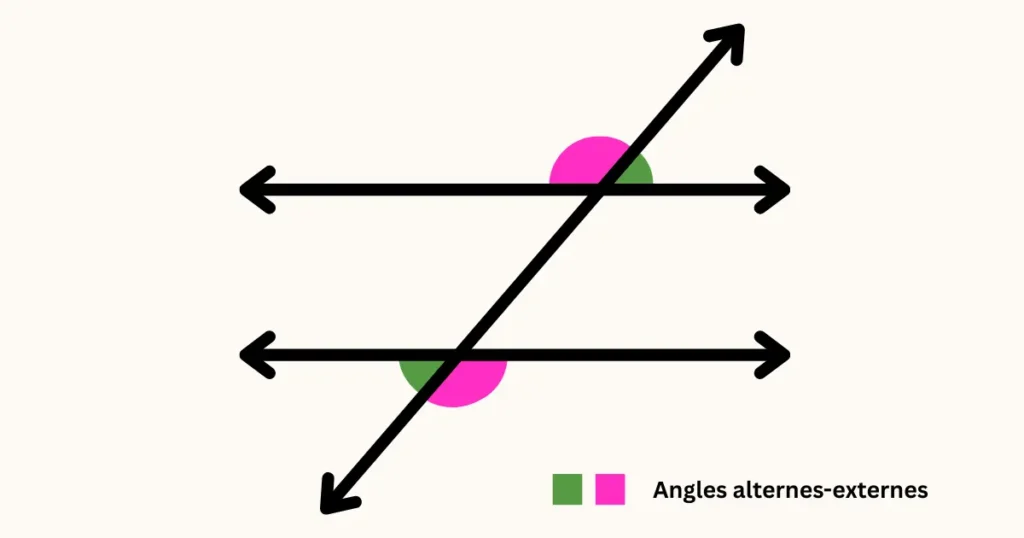
Définition des angles alternes-externes
- Ils sont à l’extérieur des deux droites parallèles.
- Ils sont de part et d’autre de la transversale, donc l’un est en haut, l’autre en bas, mais à l’extérieur.
- Ils ne partagent pas de sommet et se retrouvent dans une configuration en « Z » à l’extérieur.
👉 Ils sont égaux si les droites sont parallèles. Moins connus que les alternes-internes, ils respectent pourtant la même logique.
Exemple :
Quand les utiliser ?
- Pour prouver l’égalité de deux angles extérieurs.
- Pour compléter une démonstration géométrique.
- Pour repérer des angles dans des figures ouvertes.
Quiz : testez vos réflexes géométriques
1. Les angles alternes-internes sont toujours…
A) égaux
B) opposés par le sommet
C) sur la même droite
2. Les angles correspondants sont dans une position :
A) différente
B) identique
C) sans lien
3. Les angles alternes-internes se trouvent…
A) à l’extérieur
B) du même côté de la transversale
C) de part et d’autre de la transversale
4. Une paire d’angles correspondants est…
A) à l’intérieur des deux droites
B) de même côté, un intérieur, un extérieur
C) opposée par le sommet
5. Peut-on utiliser les angles alternes-internes pour démontrer qu’un quadrilatère est un parallélogramme ?
6. Est-il possible que deux angles correspondants soient inégaux ?
Réponses au quiz
| N° | Question | Réponse correcte | Explication |
|---|---|---|---|
| 1 | Les angles alternes-internes sont toujours… | ✅ A) Égaux | Si les droites sont parallèles, les angles alternes-internes sont toujours égaux. |
| 2 | Les angles correspondants sont dans une position… | ✅ B) Identique | Même côté de la transversale, même position sur les droites. |
| 3 | Les angles alternes-internes se trouvent… | ✅ C) De part et d’autre de la transversale | Ils sont à l’intérieur des droites, mais de côtés opposés de la transversale. |
| 4 | Une paire d’angles correspondants est… | ✅ B) De même côté, un intérieur, un extérieur | L’un est à l’intérieur, l’autre à l’extérieur, mais du même côté de la transversale. |
| 5 | Peut-on utiliser les alternes-internes pour prouver qu’un quadrilatère est un parallélogramme ? | ✅ Oui | L’égalité des angles alternes-internes permet de démontrer que deux côtés sont parallèles. |
| 6 | Est-il possible que deux angles correspondants soient inégaux ? | ✅ Oui, si les droites ne sont pas parallèles | L’égalité des angles correspondants suppose le parallélisme. Sinon, ils peuvent être différents. |
Exercice explicatif avec correction

Ennoncé (angle noté α = 38°)
On considère deux droites parallèles (d₁) et (d₂) coupées par une même transversale (t).
À l’intersection de (t) avec (d₁), l’angle situé en haut à gauche mesure α = 38 °.
- Quelle est la mesure de l’angle correspondant sur la droite (d₂) ?
- Quelle est la mesure de l’angle alterné‑interne associé ?
- Quelle est la mesure de l’angle alterné‑externe associé ?
- Les trois angles ainsi obtenus ont‑ils la même mesure ? Justifie ta réponse en utilisant les propriétés des angles formés par une transversale coupant deux parallèles.
Indice : Observe la position « haut / bas » et « gauche / droite » par rapport à la transversale, puis applique les règles :
– angles correspondants ;
– angles alternes‑internes ;
– angles alternes‑externes.
Correction
| Type d’angle | Position | Mesure |
|---|---|---|
| Correspondant | même quadrant (haut‑gauche) sur (d₂) | 38 ° |
| Alterné‑interne | intérieur des parallèles, de l’autre côté de (t) (bas‑droite sur (d₂)) | 38 ° |
| Alterné‑externe | extérieur des parallèles, de l’autre côté de (t) (bas‑droite sur (d₁)) | 38 ° |
Justification : Quand deux droites sont parallèles, une transversale crée des couples d’angles correspondants, alternes‑internes et alternes‑externes qui sont toujours égaux. Ici, chaque angle demandé partage la même mesure que l’angle initial α.
FAQ – Vos questions fréquentes
Les angles alternes-internes sont-ils toujours égaux ?
Oui, si et seulement si les droites sont parallèles. Si elles ne le sont pas, les angles peuvent avoir des mesures très différentes.
Comment reconnaître un angle correspondant rapidement ?
Il suffit de comparer la position relative par rapport à la transversale : même côté, même coin, mais à l’intérieur et à l’extérieur. C’est un repère très visuel.
Et les angles opposés par le sommet ?
Ce sont deux angles formés par l’intersection de deux droites, qui se regardent. Ils partagent un sommet et sont toujours égaux, quelle que soit l’orientation des droites.
Existe-t-il d’autres types d’angles particuliers ?
Oui, comme les angles alternes-externes, les angles adjacents, les angles complémentaires ou supplémentaires. Tous ont leur importance dans l’étude des figures.
Peut-on avoir des angles égaux sans que les droites soient parallèles ?
Oui, mais cela relève de cas particuliers. Les règles des angles alternes-internes et correspondants ne sont valables que dans le cas des droites strictement parallèles.
Résumé à retenir
| Type d’angle | Position | Égaux si droites // ? | Astuce visuelle | Utilité |
|---|---|---|---|---|
| Alternes-internes | Intérieur, en Z | ✅ Oui | « Zigzag » | Démontrer égalité d’angles, constructions. |
| Correspondants | Même position, en F | ✅ Oui | « F visuel » | Figures symétriques, justifications. |
| Opposés par le sommet | Croisés, même sommet | ✅ Oui | Croix « X » | Intersection de droites. |
| Alternes-externes | Extérieur, en Z | ✅ Oui | « Z à l’extérieur » | Cas particuliers. |
🧾 Conclusion
Maîtriser les angles alternes-internes, alternes-externes et correspondants est une clé pour progresser en géométrie. Ces configurations permettent de reconnaître des égalités et de résoudre des problèmes complexes avec méthode. En les visualisant avec des lettres comme Z, F ou X, tu gagneras en rapidité et en précision. Ce sont des repères puissants pour vérifier le parallélisme ou construire des figures rigoureuses. Avec un peu de pratique, ces notions deviennent naturelles. Reviens à ce guide dès que tu as un doute ! Et surtout, amuse-toi à repérer ces angles dans ton environnement : escaliers, croisements de rues ou charpentes. La géométrie est partout autour de nous